Improving Mathematical Disposition and Achievement In Students (and Staff!)
- markhansen1983
- Sep 23, 2020
- 5 min read
Updated: Sep 26, 2020
Note: This is an extended version of an article that appeared in the Mathematics Association of NSW (MANSW) in 2018.
“I sell a product to a market that doesn’t want it, but it is forced by law to buy it”
Dr Dan Meyer, Mathematics Teacher, 2010
In my work as a primary classroom teacher, Master Teacher and now part of the leadership team at our school, I have generally witnessed a strong correlation between a student’s mathematics disposition and their aptitude for the subject. As implied in the above quote from Dr Dan Meyer (2010), oftentimes students struggle during Numeracy lessons because they see no sense in it, and educators are faced with dual concerns: rectifying misconceptions students may have, and improving student disposition to enable them to utilise this mathematical knowledge to solve problems in real-life contexts (Askew, 2012).
The school being discussed, and in which I am currently employed, is a P-6 primary school with an ICSEA ranking of 960 (27th percentile) and roughly 720 students. Prior to my appointment as Numeracy Coach: North Coast Region (then Master Teacher -Numeracy) in Semester 2, 2014, there was an over-reliance on explicit teaching, with little to no pre-testing to determine student’s instructional level and areas of interest. NAPLAN data was in the red, but, with a supporting administrative team and a stable teaching population the challenge to improve was met, with the “School Improvement Hierarchy” (Figure 1) later used as a tool to aid conversations.

(Figure 1: School Improvement Hierarchy (Education Queensland 2018))
From this junction, and with the direction of the North Coast PEAC's (Principal Education Advisors) teachers were released with their year level colleagues on alternating fortnights to diagnose and plan responses to student mathematical misconceptions, with myself in the role as a maths coach throughout the rest of the week. The focus, at least initially, was on mathematical ‘activators’ designed to get students rolling dice, using playing cards and re-engaging with mathematics. There was also a focus on student reasoning and an increase in teacher questioning and expectations.
The Grattan Report of July 2015 established that although schools are not short of data, teachers might not be gathering this at the right time nor making the best use of the information (Goss & Hunter, 2015). In addition to mandated data collection methods (whose results may be misunderstood or underused), teachers utilised purpose designed diagnostics to determine student misconceptions and take back ownership of the curriculum; investing time on activities students required for developmental understanding.
We were guided by Vygotsky’s claim that children need experiences within their zones of proximal development (ZPD); that is, experiences they cannot do without guidance, but can do with guidance (Berk & Winsler, 1995). Aligned with this, and specifically for mathematics, Meyer (2010) makes a bold call to action which includes the following guidelines for teachers:
1. Use multimedia
2. Encourage student intuition
3. Ask the shortest question you can
4. Let students build the problem
5. Be less helpful
We took heed of Dan Meyer’s directives through the use of 3-Act tasks (Meyer, 2011) many of which we developed ourselves, and others which are freely available online. Throughout these experiences students spent considerable time in the “zone of confusion” (Clarke, Cheeseman, Roche & Van Der Schans, 2014, p. 58) which Russo (2020) found was integral to the learning experience. Hindsight has also shown that these tasks align with the design characteristics of challenging tasks (Russo, 2020).
As some people may have found through the recent enforced remote learning model, in some ways it can be easier to teach mathematics from home.
The challenge for us as educators in mathematics has always been how do we bring the mathematics in the ‘real-world’ into schools and make sure it still seems real?
Where possible, this was countered by capitalising on regular school events such as discos, Mother’s Day stalls, tuckshop menus, building of new playgrounds to build mathematical experiences relevant to students and in line with our new-found mathematical philosophy.
Our pedagogical doctrine became “Teaching Primary Mathematics” (Booker et al., 2014), a comprehensive developmental understanding of mathematics. We also relied on “Practices for Orchestrating Mathematical Discussions” (Stein & Smith, 2011) which promotes that teachers anticipate, monitor, select, sequence and connect mathematical ideas during a mathematical task.
With an increase in teacher knowledge, our school created school wide planners which respond to “Five Questions for Teachers”:
1. What am I teaching?
2. Why am I teaching it?
3. How will I teach it?
4. How will I know when all students have learned it?
5. What’s next?
(Sharratt & Fullan, 2012).
These planners ensure year level consistency, and result in all teachers responding to student’s current ability. The classrooms in which our teachers now teach see more student intuition and reasoning, more teacher confidence and flexibility within the curriculum, as well as teachers relying on high-yield proven strategies such as developmentally appropriate materials, Number Talks and Open-Ended Mathematics activities. Likewise with the aforementioned 3-Act tasks, these are inclusive and enable all students to enter with possibilities of extension.
Key success points from a data point of view include significant reduction in the number of students in the bottom bands of NAPLAN, Mean Scale Scores which are now comparable with the National average (Table 1), and high retention rates for students getting Upper Two Banding in year 5 from year 3. Anecdotally student and teacher disposition has improved as has our A-E data and NAPLAN alignment with this.
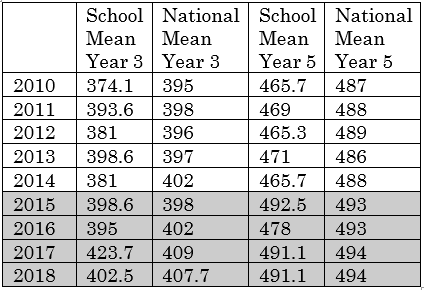
(Table 1: NAPLAN School MSS vs National MSS)
Reflections at this point involve the realisation that Administrative support, both time and financial, is paramount to success (we were fortunate in this respect). Ensuring the right people are in the right place, pursuing a growth mindset and having a clear succession plan in place proved pertinent.
We were fortunate to be a part of such a high-functioning and to have experts to which we could turn also. We encourage anyone with a similar task to network widely: we organised a number of visits from mathematical consultants over this period, and we continue to liaise with professionals in the field. It is always a privilege to connect either physically or remotely with colleagues, as after all, ‘teaching is a team sport’.
Askew, M. (2012). Transforming primary mathematics. London: Routledge.
Berk, L., & Winsler, A. (1995). Scaffolding children's learning. Washington: National Association for the Education of Young Children.
Clarke, D., Cheeseman, J. Roche, A., & Van Der Schans, S. (2014). Teaching Strategies for Building Student Persistence on Challenging Tasks: Insights Emerging from Two Approaches to Teacher Professional Learning. Mathematics Teacher Education and Development, 16(2), 46-70.
Education Queensland. (2018). Every Student Succeeding: State Schools Strategy 2018-2022. Retrieved 30 July 2018, from http://education.qld.gov.au/corporate/about/pdfs/state-schools-strategy-2018-2022.pdf
Goss, P., & Hunter, J. (2015). Targeted teaching: How better use of data can improve student learning. Grattan Institute. Retrieved 17 March 2016, from http://grattan.edu.au/wp-content/uploads/2015/07/827-Targeted-Teaching.pdf
Hattie, J. (2009). 138 influences related to achievement - Hattie effect size list. Retrieved 18 February 2015, from http://visible-learning.org/hattie-ranking-influences-effect-sizes-learning-achievement/
Meyer, D. (2010, March 6). Math curriculum makeover [Video file]. Video posted to https://www.youtube.com/watch?v=BlvKWEvKSi8
Meyer, D. (2011). The Three Acts Of A Mathematical Story. Retrieved 9 May 2020, from https://blog.mrmeyer.com/2011/the-three-acts-of-a-mathematical-story/
Russo, J. (2020). Designing and scaffolding rich mathematical learning experiences with challenging tasks. Australian Primary Mathematics Classroom, 25(1), 3.
Sharratt, L., Fullan. M. (2012). Putting FACES on the Data. Ontario: Corwin.
Stein, M., & Smith, M. (2011) 5 Practices for Orchestrating Mathematical Discussions. USA: National Council of Teachers of Mathematics. Retrieved from



Comments